PID Controller Arduino - Proportional Integral Derivative explanation

This article will provide an accurate idea of the structure and functioning of a PID controller. However, going into the details, let's get an introduction to PID controllers. PID controllers are found in a very wide range of applications for industrial process control system. Approximately 95% of the closed loop operations of the industrial automation sector use PID controllers.

PID stands for proportional integral derivative. These three controllers are combined in such a way that they produce a control signal. As a feedback controller, it provides control output at desired levels. Before the invention of the microprocessor (MC), PID controller control was implemented by analog electronic components. But now all PID controllers are processed by microprocessors (CPU). Programmable logic controllers also have built-in PID controller instructions. Due to PID controllers flexibility and reliability, they are traditionally used in process control applications.

What is a PID controller?

The term PID stands for proportional integral derivative and is one type of device used to control various process variables such as pressure, flow, temperature and speed in industrial applications. In this controller, a control loop feedback device is used to regulate all process variables.

This type of control is used to drive a system in the direction of an objective location other than that plane. It is almost ubiquitous for temperature control and is used in scientific processes, automation, and countless chemicals. In this controller, closed-loop feedback is used to keep the real output from a method like close to the target otherwise output at the anchor point if possible. In this article, the design of the PID controller is discussed with the control modes used in it such as P, I & D.

The first PID controller was developed and created by Elmer Sperry. Then a TIC (Taylor Instrumental Company) for an earlier fully tunable pneumatic controller was implemented in 1933. After a few years, control engineers eliminated the steady-state error present inside proportional controllers by resetting the end to some spurious value until the error was not Zero.

The reset included the error known as the Integrated Proportional Controller. Then, in 1940, the first pneumatic PID controller was developed by a derivative procedure to reduce bypass problems.

In 1942, Ziegler & Nichols introduced tuning rules for the discovery and setting of appropriate parameters for PID controllers by engineers. Finally, PID automatic controllers were widely used in industries in the mid 1950's.

A closed loop system such as the PID controller includes a feedback control system. This smart system evaluates the feedback (smart loop) variable using a fixed point to generate an error signal. Based on this, it changes the output of the system. This action will continue until the error reaches zero otherwise the value of the feedback variable becomes equivalent to a fixed point.

This controller provides good results compared to the ON/OFF type controller. In the ON / OFF type controller, only two conditions for managing the system can be obtained. Once the value of the operation is less than the fixed point, it will run. Likewise, it will be turned off once the value is higher than a constant value. The output is unstable in this type of controller and it will swing frequently in the fixed point region. However, this controller is more stable and accurate compared to the ON/OFF type controller.

With a simple, low-cost ON-OFF controller, only two states can be controlled, such as full on or full off. It is used for a finite control application where these two control states are sufficient for the control objective. However, the oscillatory nature of this control limits its use, and thus it is being replaced by PID controllers.

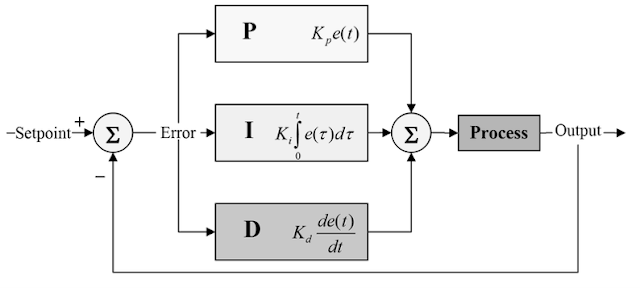
The PID controller maintains the output (O) so that there is zero (0) error between the variable process and the setpoint/output required by closed loop operations. The PID uses three basic control behaviors that are described below.

Proportionality or P-observer gives an output proportional to the current error e (t). Compares the desired or specified point with the actual value or the value of the feedback process. The resulting error is multiplied by a proportional constant to get the result. If the error value is zero, this controller output will be zero.

This PID controller requires manual bias or reset when used alone. This is because it never reaches a steady state. It provides stable operation but always maintains steady state error. The response rate increases when the relative constant Kc increases.

I-control

Due to the limitation of PID controller where there is always an offset between the variable process and the setpoint, controller I is needed, which provides the action necessary to eliminate the steady-state error. It consolidates the error over a period of time until the error value reaches zero. It carries the value to the final controller at which the error becomes zero.

PI . control

Integrated control reduces its output when a negative fault occurs. It limits the response speed and affects the stability of the system. The response speed is increased by decreasing the integral gain, Ki.

In the above figure, as the gain of the controller I decreases, the steady-state error also continues to decrease. For most cases, the PI controller is specifically used when a high-speed response is not required.

While in use of the PI controller, the output of the I-controller is somewhat range-limited to overcome integrated wind conditions as the integrated output continues to increase even at zero error, due to the non-linearity of the plant.

D-control

The I-controller does not have the ability to predict the future behavior of an error. So it reacts normally once the set point is changed. D-controller overcomes this problem by anticipating the future behavior of the error. Its product depends on the rate of change of the error with respect to time, multiplied by the constant derivative. It gives a starting kick to the output thus increasing the response of the system.

PID control

In the above figure response to D, the controller is more, compared to the PI controller, and the production settling time is also reduced. Improves system stability by compensating for the phase delay generated by the controller I. Increasing the gain of the derivative increases the response speed.

So we finally noticed that by combining these three controllers we can get the desired response of the system. Different manufacturers design different PID algorithms.

PID controller types

PID controllers are categorized into three types as ON/OFF, proportional, and standard-type controllers. These controllers are used based on the control system, and the user can use the controller to organize the method.

ON / OFF control

The on and off control method is the simplest type of device used to control the temperature. The output of the device may be on / off by not having a centralized state. This controller will turn on the output once the temperature crosses the fixed point. A limit controller is a specific type of on/off controller that uses a shut-off relay. This relay is reset manually and is used to turn off a method once a certain temperature is reached.

proportional control

This type of controller is designed to remove the connected rotation through on/off control. This PID controller will reduce the normal power supplied towards the heater once the temperature reaches the fixed point.

This controller has one feature to control the heater so that it does not exceed the fixed point but will reach the fixed point to maintain a constant temperature.

This proportional action can be achieved by turning the output on and off for small periods of time. This time proportion will change the ratio from the on-time to off-time for temperature control.

Standard type PID controller

This type of PID controller will integrate proportional control through integrated and derivative control to help the unit automatically compensate for adjustments within the system. These modifications, the integral and the derivative are expressed in units of time.

These controllers are also referred by reciprocity, RATE & RESET in return. PID conditions must be modified separately, otherwise they are set to a particular system with trial as well as error. These controllers will provide the most accurate and stable control of the three types of controllers.

Real-time PID control

Nowadays, there are various types of PID controllers available in the market. These controllers are used for industrial control requirements such as pressure, temperature, level and flow. Once these parameters are controlled by the PID, the choices include a separate PID controller or either a PLC.

These separate controllers are used wherever two loops need to be inspected, as well as otherwise controlled in circumstances where it is complex to have access through larger systems.

These controllers provide different options for single and dual control. Independent type PID controllers provide several fixed point configurations to produce many independent alarms.

These standalone controllers mainly consist of PID controllers from Honeywell, temperature controllers from Yokogawa, and auto-tuning controllers from OMEGA, Siemens, and ABB.

PLCs are used as PID controllers in most industrial control applications. The arrangement of PID blocks can be done within PACs or PLCs to give superior options for precise PLC control. These controllers are smarter and more powerful compared to separate controllers. Each PLC includes a PID block within the program programming.

Adjustment methods

Before the PID controller can be operated, it must be tuned to suit the dynamics of the process to be controlled. Designers give default values for the terms P, I and D, and these values cannot give the desired performance and sometimes lead to instability and slow control performance. Various types of tuning methods have been developed for tuning PID controllers and require a lot of attention from the operator to determine the best values for relative, integral and derived gains. Some of these are given below.

PID controllers are used in most industrial applications, but one must know the settings of this controller to adjust them correctly to generate the preferred output. Here, tuning is nothing but a procedure for receiving an optimal response from the controller by defining the best relative gains and integral and derived factors.

The desired output of the PID controller can be obtained by adjusting the controller. There are different techniques available to get the desired output from the controller such as trial and error curve, Zeigler-Nichols and process interaction curve. The most commonly used methods are trial and error, Ziegler Nichols, etc.

Trial and error method: It is a simple way to set the PID controller. While the system or controller is working, we can adjust the controller. In this method, first, we have to set the values of Ki and Kd to zero and increase the relative term (Kp) until the system reaches an oscillatory behaviour. Once it oscillates, adjust Ki (integral term) so that the oscillations stop and finally adjust D to get a quick response.

Process reaction curve technology: It is an open loop tuning technology. Produces a response when a step entry is applied to the system. Initially, we have to apply some control output to the system manually and we have to record the response curve.

Next, we need to calculate the slope, dead time and rise time of the curve and finally replace these values in the equations P, I and D to get the gain values for the PID terms.

PID controller Process reaction curve

Zeigler-Nichols method: Zeigler-Nichols suggested closed-loop methods for tuning the PID controller. This is the continuous rotation method and the damped oscillation method. The procedures for both methods are the same but the oscillation behavior is different. In this, first, we have to set the p-controller constant, Kp to a certain value while Ki and Kd values are zero. The relative gain is increased until the system oscillates at a constant amplitude.

The gain at which the system produces constant oscillations is called the final gain (Ku) and the period of oscillations is called the final period (Pc). Once it is accessed, we can enter the values of P, I, and D into the PID controller by a Zeigler-Nichols table that depends on the controller being used such as P, PI, or PID, as shown below.

PID Controller Arduino - Proportional Integral Derivative explanation